Skip to content Skip to sidebar Skip to footer
Home / Are Student Marks Discrete or Continuous

Are Student Marks Discrete or Continuous

Post a Comment

Is my data continuous or discrete?

View All Blogs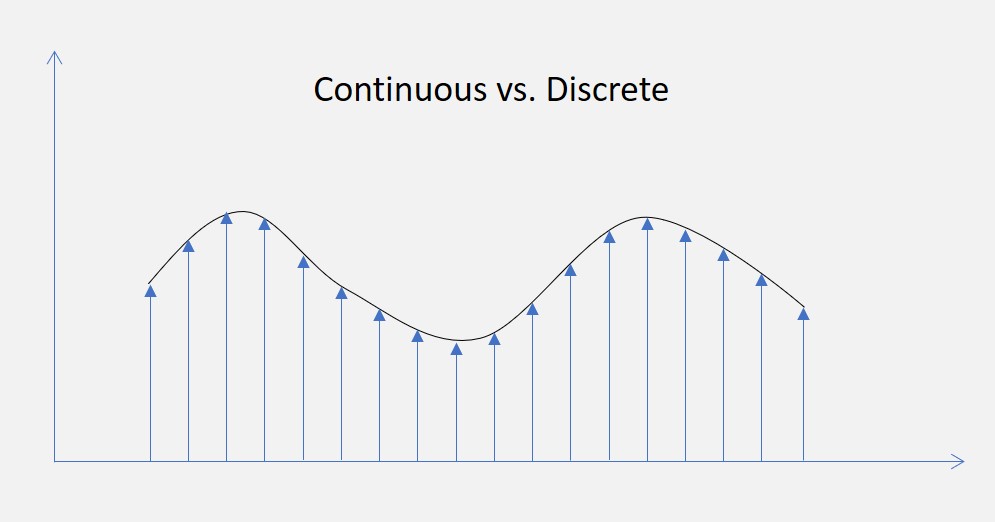

Types of Data

When analyzing data, often times we need to know if our data set is continuous or discrete. The primary reason for this is to identify which statistical tool or methodology we need to use to analyze the data. If the data set is continuous, we need to use one set of analytical tools or methods and if the data is discrete, we would have to use a different set of tools or methods. I have seen several places in literature, where this determination of the type of data is made incorrectly and as a result, the wrong analysis was done to the data causing an error in the analysis and conclusions. In this blog, we will distinguish between the different types of data and hopefully make it clear how you can identify the type of data you have.

What is data?

Data is any factual information or measurement that is collected and used for making a decision, reasoning, or any calculation. We need to process the data in order to extract and understand the information that the data is telling us. Data is the language of the process which is telling us what is happening with the process.

Different types of data

There are various ways of classifying the data, but we will use the following simple classification shown in the figure below. Data Type Classification

Qualitative Data

Data can be either qualitative (expressed as text – example color of the product, description of the product features) or quantitative (expressed as numbers – number of items with color green is 4). For example, if we are describing a cup of coffee, qualitative data could be "the coffee tastes great" and quantitative data could be "the temperature of the coffee is 76 degree Celsius" or "the coffee costs $12.50".

Most of the time, when we collect data, we try to collect quantitative data so that we can draw better conclusions from the data. However, on surveys and from other sources we also collect qualitative data as well. When we collect the quantitative data, we can further classify them into two types: discrete and continuous.

Discrete Data

Discrete data is data for which all values on the real number line are not possible – only certain values are possible. For example, the grade you receive in your school exam (A, B, C, D, or E) is an example of discrete data because your grade can only take on one of these 5 possible values and nothing else. Discrete data can be further sub-divided into three categories: binary, nominal and ordinal.

Binary Data: A binary data only takes on two possible values. For example, lamp is on or lamp is off, answer is true or false, 0 or 1, yes or no etc. If you collect the data about the number of reports that have an error that would be an example of binary data. Binary Data
Nominal Data: Nominal data set can take on more than 2 values but these values are not ordered – there is no natural ordering or comparison of these values. For example, nationality, occupation, region, defect category etc. If you collect the data about different types of errors made by the department that would be an example of nominal data. Nominal Data
Ordinal Data: Ordinal data also takes on multiple values but these are naturally ordered – you can conclude that one is better than the other. For example, grades in an exam, results of the running race, customer survey results etc. For example, if you perform a survey and there are five responses to the survey question "Bad", "Below Average", "Average", "Above Average", and "Excellent". These five responses are ordered so this would be an example of ordinal data. Ordinal Data

Continuous Data

In a continuous data set, any value is theoretically possible. For example, you could get a value such as 2.37983. All values on the real number line could be possible data values. For example, the length of a table could possibly take on any value. Only the instrument measuring may limit the number of decimal places we could report. If we had a better measuring instrument, any value is theoretically possible. Examples of continuous data are those that are typically measured like temperature, pressure, humidity, length, time etc. Continuous data can be further classified as measured on an interval scale or a ratio scale.

Interval Scale: Interval scale is those values which does not have a natural zero. You cannot take a ratio of these numbers – for example the temperature of the room measured in Celsius.

Ratio Scale: Ratio scale is those values that have a natural zero. For example, temperature of the room measured in Kelvin. No temperature can go below 0 K. For example, the average time taken to respond to a customer survey questionnaire shown below is an example of continuous data. Continuous Data

Questions

Let's look at some examples to see if we can classify the different types of data. Classify the following as either continuous or discrete data.

  • Number of road accidents in a month in Chicago
  • Customer satisfaction survey results (measured on a 1-5 scale)
  • Time taken to deliver a product to the customer in days
  • Percentage of people who are absent in a class
  • Sales revenue of a product for each quarter (measured in $)

The answers to the above questions are: a) Discrete, b) Discrete, c) Continuous, d) Discrete, and e) Continuous. For the number of road accidents, it is discrete because we can only have an integer number of road accidents. For example, you can have either 2 or 3 accidents but you cannot have 2.3 accidents in a month. For customer satisfaction survey, it is discrete because you can only have values from 1, 2, 3, 4, or 5 but not any number in between. For Time taken to deliver product, you could theoretically have 2.3 days of delivery or any value is possible, so it is continuous. For the percentage of people absent in the class, it is a ratio of two discrete numbers and hence should be treated as discrete. All values are not possible – for example if there are 10 people in a class and 1 is absent, then you get 0.1 (10% absent) or if 2 people are absent you get 0.2 (20% absent), you cannot get any values in between. Hence, this should strictly be treated as discrete. Finally, for the sales revenue, it is measured in $$ and hence should be treated as continuous any value is theoretically possible.

Always look at the underlying nature of the data to determine if the data set is continuous or discrete. If the underlying data is discrete, then the data should be considered as discrete. Thus, ratio of two discrete numbers should be treated as discrete, for example, % of items fixed right the first time. Ratio of discrete and continuous values should be treated as continuous, for example average time to repair a TV set.

Follow us on LinkedIn to get the latest posts & updates.

parkeraffied.blogspot.com

Source: https://www.sigmamagic.com/blogs/is-my-data-continuous-or-discrete/

Post a Comment for "Are Student Marks Discrete or Continuous"